Listas, operadores y aritmética.- PROLOG cap-3

INTRODUCCIÓN.

Tal y como hemos venido trabajando, en esta ocasión nos toca trabajar mas a profundidad, como son las listas, operadores y la aritmética, los lenguajes como java, c, c++, etc. etc, sabemos que manejan listas porque lo hacen justamente para facilitar operaciones complejas y sobre todo para almacenar cierta información a procesar, ¿En prolog necesitamos listas, operadores o la aritmética? si, si las necesitamos porque trabajamos con objetos estructurados tipo árbol, ademas que tenemos que lidiar con los de tipo operador  esto y mas vamos a trabajar.

Listas, operadores y aritmética.

3.1. Representación de listas.

La "lista" es una estructura de datos ampliamente utilizada en la programación no numérica. Una lista es una secuencia de cualquier número de elementos, tales como los objetos ana, tenis, tomás, eskí. Esta lista se puede escribir en Prolog como:

[ ana, tenis, tomás, eskí ]

Sin embargo ésta es solamente la apariencia externa de las listas. En Prolog todos los objetos estructurados son árboles y las listas no son una excepción.

¿Cómo puede una lista representarse como un objeto Prolog? Tenemos que considerar dos casos: si la lista está ó no vacía. En el primer caso la lista se escribe como un átomo Prolog : []. En el segundo caso la lista puede verse como formada por dos cosas:

(1). el primer elemento, llamado "cabeza" de la lista.

(2). los elementos restantes, llamados en conjunto: "cola" de la lista.

Para el ejemplo anterior : [ ana, tenis, tomás, eskí ]

la cabeza es : ana

la cola es : [ tenis, tomás, eskí ].

En general, la cabeza puede ser cualquier cosa (cualquier objeto Prolog, por ejemplo, un árbol ó una variable); la cola tiene forzosamente que ser una lista. La cabeza y la cola se combinan en una estructura con un functor especial. El símbolo para este functor depende de la implementación de Prolog. Asumiremos que se trata del punto [.] .

.( Cabeza, Cola)

Debido a que la cola es a su vez una lista, se tratará de una lista vacía ó una lista con cabeza y cola. Por lo tanto para representar listas de cualquier longitud no se necesita establecer ningún principio adicional. El ejemplo anterior se representa con el término:

.( ana, .( tenis, .( tomás, .( eskí, [] ))))

la siguiente figura muestra la estructura de árbol que le corresponde :

Observe que la lista vacía aparece en el término anterior. Esto es porque la última cola es una lista con un sólo elemento:

[ eskí ]

esta lista tiene a su vez a la lista vacía como cola :

[ eskí ] = .( eskí, [] )

3.2. Operaciones sobre listas.

Las listas se pueden utilizar para representar conjuntos aunque se debe tomar en cuenta que existen diferencias: el orden de los elementos en un conjunto no interesa mientras que en una lista sí, además los objetos se pueden repetir en una lista y en un conjunto no. Aún con estas diferencias, las operaciones más frecuentes sobre listas son semejantes a las operaciones sobre conjuntos:

Pertenencia a una lista.

Implementaremos la relación miembro como:

miembro( X, L)

donde X es un objeto y L es una lista. La meta miembro( X, L) es cierta si X es miembro de la lista L, por ejemplo :

miembro( b, [ a, b, c])

es cierta, y

miembro( b, [ a, [ b, c] ])

no es cierta, pero

miembro( [ b, c], [ a, [ b, c]])

es cierta. El programa para la relación de pertenencia se puede basar en la siguiente observación:

X es un miembro de L si,

(1) X es la cabeza de L, ó

(2) X es un miembro de la cola de L.

Esto puede representarse con dos cláusulas, la primera es un hecho simple y la segunda es una regla:

miembro( X, [ X | Cola]).

miembro( X, [ Cabeza | Cola] ) :-

miembro( X, Cola).

Concatenación.

Para la operación de concatenación definiremos la relación:

         concat( L1, L2, L3)

donde L1 y L2 son dos listas y L3 es su concatenación. Por ejemplo:

         concat( [a,b], [c,d], [a,b,c,d])

es cierta, pero

         concat( [a,b], [c,d], [a,b,a,c,d])

es falsa. En la definición de concat tendremos dos casos dependiendo del primer argumento L1:

(1)   Si el primer argumento es la lista vacía entonces el segundo y el tercer argumento deben ser la misma lista:

concat( [], L, L).

(2). Si el primer argumento de concat no es una lista vacía, entonces tiene cabeza y cola, es decir, se ve como :

[ X | L1]

la figura siguiente ilustra la concatenación de [X|L1] y otra lista L2 :

el resultado de la concatenación es la lista [X|L3] donde L3 es la concatenación de L1 y L2. En Prolog lo representamos:

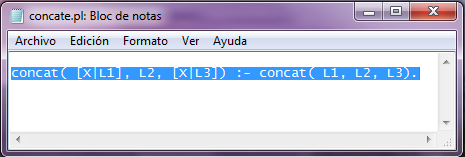
concat( [X|L1], L2, [X|L3]) :-

concat( L1, L2, L3).

En Prolog queda  así----------->

?- concat( [a,b,c], [1,2,3], L).

L = [a,b,c,1,2,3]

?- concat( [a,[b,c],d],[a,[],b],L).

L = [a, [b,c], d, a, [], b]

[Inf. Tomada por el Autor:  Edgar Altamirano Carmona  Universidad  Autónoma  de  Guerrero.]

Ejercicios.

1. Escriba una meta, usando concat, para eliminar los tres últimos elementos de una lista L produciendo otra lista L1. Recomendación: L es la concatenación de L1 y una lista de tres elementos.

eliminar3[L,L1]:-concat([X,Y,Z],L1,L).

concat([],L,L).

concat([X|L1], L2,[X|L3]):-concat(L1,L2,L3).

2. Escriba una secuencia de metas para eliminar los tres primeros elementos y los tres últimos elementos de una lista L produciendo la lista L2.

elimina([],_X,[]):-!.

elimina([X|L],X,Z):- elimina(L,X,Z),!.

elimina([R|L],X,[R|Z]):- elimina(L,X,Z),!.

Pruebas realizadas:

3. Defina la relación:

ultimo( Elemento, Lista)

de tal modo que Elemento sea el último elemento de la lista Lista. Escriba dos versiones: (a) usando la relación concat, y (b) sin usarla.

ultimo(X,[_|L1]):- ultimo(X,L1).

ultimo(X,[X]).

En las pruebas nos muestra si es true que el elemento que se indica es el último de la lista o false si no lo es.

Adicionar un elemento.

Para adicionar un elemento a una lista, se puede colocar este nuevo elemento al frente de la lista de tal modo que sea la nueva cabeza de la lista :

aumentar( X, L, [X|L]).

Eliminar un elemento.

Para eliminar un elemento X de una lista L se puede programar la relación:

eliminar( X, L, L1)

donde L1 es igual a la lista L con el elemento X removido. Esta relación se puede definir de manera similar a la relación de pertenencia, tendremos nuevamente dos casos posibles :

(1). Si X es la cabeza de la lista, entonces el resultado después de la eliminación es la cola de la lista.

(2). Si X está en la cola entonces deberá eliminarse de la cola.

En Prolog:

pruebas realizadas nos dan los siguientes resultados:

3.3. Notación de los operadores.

En matemáticas estamos acostumbrados a escribir expresiones como:

2 * a + b * c

donde + y * son operadores, 2,a,b y c son argumentos. Decimos que estos operadores son infijos porque aparecen entre dos argumentos. Estas expresiones se pueden representar como árboles y se pueden escribir como términos de Prolog con los símbolos + y * como functores:

+( *( 2, a), *( b, c))

Prolog acepta también la notación infija pero recuerde que ésta es solamente su representación externa y será automáticamente convertida a la forma normal anterior de Prolog (árbol). Es decir, si escribimos en la forma a + b, Prolog lo manejará exactamente igual que si hubiésemos escrito +( a, b).

El principal functor será siempre el operador con la más alta precedencia.

Un programador puede definir además sus propios operadores. Por ejemplo podemos definir los operadores tiene y soporta como operadores infijos y poder escribir después en nuestros programas hechos como:

pedro tiene informacion.

el_piso soporta la_mesa.

estos hechos resultan exactamente equivalentes a :

tiene( pedro, informacion)

soporta( el_piso, la_mesa)

La manera en cómo definimos operadores nuevos es insertando en el programa tipos especiales de cláusulas conocidas como directivas que actúan para definir operadores. La definición de un operador debe aparecer en el programa antes de cualquier expresión que lo contenga. Por ejemplo, el operador 'tiene' se puede definir con la siguiente directiva:

:- op( 600, xfx, tiene).

esto le dice a Prolog que queremos utilizar 'tiene' como operador y cuyo valor de precedencia es 600 y su tipo es 'xfx' que indica que se trata de un operador infijo.

Nótese que la definición del operador no especifica ninguna operación ó acción. En principio, no se asocia ninguna operación ni dato alguno con el operador definido (excepto en casos muy especiales). Los operadores se usan normalmente como functores para combinar objetos con estructuras y no invocan acciones o datos aunque la palabra operador lo sugiera.

Los nombres de los operadores deben ser átomos y su precedencia debe

estar en un rango que dependa del sistema usado. Asumiremos un rango de 1 a 1200.

Existen tres tipos de grupos de operadores:

(1). Operadores infijos de tres tipos:

xfx xfy yfx

(2). Operadores prefijos de dos tipos:

fx fy

(3). Operadores postfijos de dos tipos:

xf yf

Explicaremos ahora la diferencia entre 'x' y 'y' pero antes debemos introducir la noción de precedencia del argumento. Si un argumento se encierra entre paréntesis ó se trata de un objeto no estructurado, entonces su valor de precedencia es 0. Si un argumento es una estructura entonces su valor de precedencia es igual a la precedencia de su functor principal. 'x' representa un argumento cuyo valor de precedencia debe ser estrictamente menor que el del operador. 'y' representa un argumento cuyo valor de precedencia es menor ó igual al del operador.

Estas reglas ayudan a reconocer expresiones ambiguas con varios operadores de la misma precedencia. Por ejemplo, la expresión:

a - b - c

se entiende normalmente como (a - b) - c y no como a - (b - c). Para realizar esta interpretación el operador '-' tiene que definirse como yfx.

Como otro ejemplo consideremos el operador prefijo not. Si not se define como fy entonces la siguiente expresión es legal :

not not p

pero si se define como fx la expresión es ilegal porque el argumento del primer not es 'not p' que tiene la misma precedencia que 'not'. En este caso la expresión debe escribirse como :

not ( not p)

Prolog contiene operadores predefinidos listos para usarse y que no necesitan definirse:

:- op( 1200, xfx, ':-').

:- op( 1200, fx, [:-,?-]).

:- op( 1100, xfy, ';').

:- op( 1000, xfy, ',').

:- op( 700, xfx, [=,is,<,>,=<,>=,==,=\=,\==,=:=]).

:- op( 500, yfx, [+,-]).

:- op( 500, fx, [+,-,not]).

:- op( 400, yfx, [*,/,div]).

:- op( 300, xfx, mod).

[Inf. Tomada por el Autor:  Edgar Altamirano Carmona  Universidad  Autónoma  de  Guerrero.]

3.4. Aritmética.

Los operadores predefinidos que se pueden utilizar para las operaciones aritméticas son :

+ adición

* multiplicación

- sustracción

/ división

mod módulo (residuo de la división entera).

Observe lo siguiente: Si preguntamos

?- X = 1 + 2.

Prolog contestará :

Y no X = 3 como podriamos esperar. La razón es simple: la expresión 1+2 solamente denota un término de Prolog donde el símbolo + es el functor y 1 y 2 son sus argumentos. No existe nada en la pregunta anterior que force a Prolog para activar la operación de la adición. Sin embargo existe un operador predefinido de Prolog “is” para resolver este problema. El operador is forza la evaluación. La manera correcta de invocar a la operación aritmética es:  

?- X is 1 + 2.

Otros ejemplos de uso del operador is son:

?- X = 3/2.

X = 1.5

?- X = 3 div 2.

X = 1

Las operaciones aritméticas también están involucradas cuando se comparan valores numéricos. Por ejemplo,

?- 277 * 37 > 10000.

Los operadores de comparación son los siguientes:

X > Y X es mayor que Y

X < Y X es menor que Y

X >= Y X es mayor o igual que Y

X =< Y X es menor o igual que Y

X =:= Y los valores de X y Y son iguales

X =\= Y los valores de X y Y no son iguales

Ejemplos.

?- 1 + 2 =:= 2 + 1. 

?- 1 + 2 = 2 + 1.

?- 1 + A = B + 2.

Ejemplo.

Dados dos enteros positivos, X y Y, encontrar el máximo común divisor D. Por ejemplo, para X=20 y Y=25 el máximo común divisor es D=5.

El máximo común divisor puede encontrarse de acuerdo a tres casos:

(1). Si X y Y son iguales, entonces D es igual a X.

(2). Si X < Y entonces D es igual al máximo común divisor de X y la diferencia Y – X.

(3). Si Y < X entonces D es igual al máximo común divisor de X y Y intercambiados.

En Prolog:

pruebas realizadas:

Ejemplo. 

Encontrar la longitud de una lista de objetos.

Pensamos en dos casos:

(1). Si la lista está vacía entonces su longitud es 0.

(2). Si no, entonces la lista puede verse como Lista = [Cabeza | Cola] y la longitud de la lista es igual a 1 mas la longitud de la Cola.

En Prolog:

?- longitud([a,b,[c,d],e], N).

N = 4

Ejercicios.

1. Defina la relación max(X,Y,Max) de tal modo que Max sea el mayor valor de los dos números X y Y.

max(X, Y, Max) :- 

X > Y, !, Max is X. 

max(X, Y, Max) :- 

Y >= X, Max is Y. 

acuérdense de aguardar su clausulas del bloc de notas con (.pl)

Pruebas realizadas:

2. Defina el predicado maxlist(List, Max) de tal manera que Max sea el mayor número de la lista List de números.

maxlist(Max, [X|Xs]):-

list_max2(Max, X, Xs).

list_max2(Max, Max, []):- !.

list_max2(X, Y, [Z|Zs]):-

Z >= Y,!,

list_max2(X, Z, Zs).

list_max2(X, Y, [Z|Zs]):-

Z =< Y,

list_max2(X, Y, Zs).

En las pruebas realizadas en prolog nos muestra el numero mayor de una lista. 

3. Defina el predicado sumlist(List, Sum) donde Sum es la suma de una lista de números dada en List.

sumlist(List,Sum).

List([X,Y,Z]).

sumlist(List,Sum):-X is Y is Z=:=Sum.

Resultado realizado en prolog.

4. Defina el predicado ordenada(List) el cual es cierto (devolverá yes) si List es una

lista ordenada de números en forma ascendente o descendente, por ejemplo,

?- ordenada(1,5,6,6,9,12).

Yes

ordenada([_]).

ordenada([X,Y|L]) :-

X =< Y,

ordenada([Y|L]).

En las pruebas realizadas nos muestra true si estan ordenada la lista de lo contrario nos muestra false.

5. Defina el predicado subsum(Set, Sum, Subset) donde Set es una lista de números, Subset es un subconjunto de esta lista y Sum es la suma de los números en Subset. Por ejemplo,

?- subsum([1,2,5,3,2], 5, Sub).

Sub = [1,2,2];

Sub = [2,3];

Sub = [5];

subsum([],0,[]).

subsum([X|L1],Y,[X|L2]) :-

Y >= X,

Z is Y-X,

subsum(L1,Z,L2).

subsum([_|L1],Y,L2) :-

subsum(L1,Y,L2).

Pruebas realizadas en prolog nos muestra estos datos.

CONCLUSIONES:

Como ya vimos la estructura sigue siendo la misma que hemos venido trabajando solo que la lógica, almenos hasta este capitulo a incrementado, aunque esto se soluciona con estudiar los operadores aritméticos, y de entender como las interpreta Prolog por lo demás son cosas básicas para prolog muy interesante al trabajar con listas ya que se vuelve una manera mas exacta de trabajar y ya nos acercamos a lenguaje real, como también se nota que es muy parecido al trabajar con otros lenguajes de programación, java, c++, c#, c, etc, etc. 

HUMOR:

facebook version (-5000) años atras.

upss OTRA VES SE NOS FUE...JJJJJ

BIBLIOGRAFIA:

Upuntes de Prolog.
Autor: Edgar Altamirano Carmona
Universidad Autónoma de Guerrero.